Мы выделили на рис. 1.14 машинное обучение как монолитную область, затем рассмотрели разные научные направления, которые используются для решения задач машинного обучения. Помимо этого, следует упомянуть классификацию машинного обучения по степени контроля за процессом обучения (контролируемое, неконтролируемое, и т. п.), а также по типу целевой переменной и решаемых задач ( рис. 1.42).
Рис. 1.42. Классификация методов машинного обучения и типов решаемых задач.
Контролируемое обучение (с учителем)
Контролируемое обучение (обучение с учителем) – это подход, при котором алгоритм обучается на входных данных, которые были размечены для решения конкретной задачи. То есть подготовленные для анализа данные изначально содержат ответ, предполагающий правильное действие, которое должна предпринять обучаемая система. Этот процесс мы уже рассмотрели выше, говоря об обучении искусственной нейронной сети.
На рис. 1.42 отмечено два типа задач в категории обучения с учителем – это классификация и регрессия.
Классификация – это одна из наиболее часто встречающихся задач в машинном обучении. Ранее мы рассмотрели использование искусственной нейросети для решения задачи классификации на рис. 1.31. Процесс заключается в том, что на вход сети подаются образцы, вычисляется выходной сигнал, который сравнивается с соответствующим значением целевого вектора (требуемого выхода сети). Векторы обучающего множества последовательно предъявляются обучаемой сети, веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемого уровня. Результатом является обученная модель, способная строить корректные прогнозы в отношении новых неразмеченных данных. Примером может служить распознавание изображений для постановки медицинского диагноза.
При этом нельзя сказать, что успехи нейросетей полностью вытеснили методы классического машинного обучения, включающего в себя целый ряд различных алгоритмов обучения, помимо нейро-сетевого. Нейросети хорошо показывают себя в задачах, где имеются большие объемы данных и признаки трудно извлечь ручным способом. Если же имеются данные небольшого объема с понятными структурированными признаками, то можно применить методы классического машинного обучения, которые мы очень кратко рассмотрим в этом курсе.
В качестве примера алгоритма классического обучения с учителем, используемого для решения задачи классификации, приведем весьма популярный метод опорных векторов (Support Vector Machine, SVM). Впервые этот алгоритм был предложен нашими соотечественниками Владимиром Вапником и Алексеем Червоненкисом в 1963 году.
Идею метода проиллюстрируем на примере задачи определения, к какому из двух изначально известных классов А и Б относится искомый объект.
Рассмотрим простейший наглядный пример (рис. 1.43), где представлены исходные точки (распределенные на плоскости по двум признакам – и ) и разбитые на два класса “А” и “Б”. Задачей классификации является предсказание принадлежности к тому или иному классу новой (не принадлежащей к известной выборке) точки на плоскости.
Чтобы пример не был абстрактным, скажем, что параметры – это возраст и доход некоторой группы людей, а задача классификации состоит в определении их принадлежности к классу А (потенциальных покупателей определенного товара) и классу Б (тех, кто товар не купит).
На рисунке построена линия, разделяющая эти два класса (разделяющая прямая). Оптимальной с точки зрения точности классификации является прямая, расстояние от которой до каждого класса максимально. Если известно положение данной прямой, то новые точки (не относящиеся к обучающей выборке) будут классифицироваться по положению относительно данной прямой, определяя их принадлежность классу A или Б.
Мы рассмотрели максимально упрощенный пример с двумя признаками. На практике их может быть произвольное число. В общем случае объект представляется вектором в n-мерном пространстве, где координаты вектора описывают его отдельные атрибуты (например, вес, возраст, доход и т. п). В пространствах произвольной размерности вместо прямых рассматривают гиперплоскости – пространства, размерность которых на единицу меньше размерности исходного. Например, в трехмерном пространстве гиперплоскость – это привычно визуализируемая двумерная плоскость.
По обеим сторонам гиперплоскости ( рис. 1.43 б ) строятся параллельные гиперплоскости. Точки данных, лежащие на одной из двух параллельных гиперплоскостей, которые определяют наибольшее расстояние, называются опорными векторами. Отсюда и происходит название метода. Чем больше расстояние между параллельными гиперплоскостями, тем меньше средняя ошибка классификатора.
Рис. 1.43. Схема, иллюстрирующая идею метода опорных векторов
Представим ситуацию, когда множество точек первого и второго класса пересекаются и разделить их прямой линией невозможно (рис. 1.44). При этом при переходе из двумерного пространства параметров в трехмерное (при добавлении еще одного параметра, являющегося комбинацией имеющихся двух) возникает возможность разнести упомянутые классы и провести искомую плоскость. Таким образом, идея метода SVM состоит в переводе исходных векторов в пространство более высокой размерности и построение гиперплоскости, оптимально разделяющей эти классы.
Рис. 1.44. Схема, иллюстрирующая идею метода опорных векторов. Источник: Jeremy Jordan
Для иллюстрации принципа работы алгоритма регрессии, упомянутой на рис. 1.42, рассмотрим линейную регрессию на примере функции одной переменной в задаче прогнозирования стоимости жилья. Предположим, что имеются исходные данные о стоимости жилья определенной площади и нам необходимо спрогнозировать цену квартиры некоторой площади, которую мы планируем приобрести. Графически это можно представить как совокупность точек, которые отражают некоторый тренд. Задача линейной регрессии состоит в том, чтобы провести прямую линию так, чтобы она наиболее точно отражала исследуемый тренд. Зная данный тренд, можно предсказать цену для любой площади.
Рис. 1.42. Линейная регрессия, метод наименьших квадратов
Прямая описывается уравнением Y = kx+b, и задача определения этой прямой сводится к нахождению параметров (коэффициентов) линейной зависимости (k и b), которые могут быть найдены путем минимизации суммы квадратов отклонений от каждой точки до нашей прямой (метод наименьших квадратов). Определив коэффициенты, мы можем провести прямую, которая обеспечивает минимальные расстояния от этой прямой до исходных точек. Получив уравнение искомой прямой, найдем значение цены квартиры при заданном значении площади .
Стоит отметить, что определение коэффициентов может быть сделано как аналитически (метод наименьших квадратов), так и с помощью оптимизационных методов. Для задач большой размерности первый способ оказывается алгоритмически более сложным, поэтому применяются методы градиентной оптимизации, такие как метод градиентного спуска.
Неконтролируемое обучение (без учителя)
К данному типу обучения относятся алгоритмы, которые обучаются на основе набора данных без каких-либо меток. В качестве примера неконтролируемого обучения можно привести кластерный анализ, где стоит задача разделить объекты на классы по неизвестному признаку. В отличие от классификации, в этом случае нет заранее известных классов. Алгоритм сам должен найти похожие объекты и объединить их в кластеры на основе некоторой заданной функции близости. Типичная задача – сегментация покупателей по предпочтениям или лояльности.
Одним из популярных алгоритмов, применяемых для решения задач кластеризации, является метод k-средних – метод, предложенный в 1950-х годах, суть которого состоит в том, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров ( рис. 1.46).
Весьма наглядное толкование метода приводит автор статьи, рассматривая задачу оптимального расположения трех ларьков в поселке. На первом шаге ставим торговые точки случайным образом и смотрим, в какой ларек кому из жителей ближе идти, выделяем три кластера – три группы людей, которым ближе идти до одного из трех ларьков. Перемещаем ларьки в сторону лучшей доступности для посетителей каждой из групп. Повторяем процедуру, то есть опять делим жителей на три кластера и вновь перемещаем ларьки до тех пор, пока не получим решение задачи.
Рис. 1.46. Схема, иллюстрирующая работу алгоритма k-средних
Другой пример, отмеченный на рис. 1.42, – это метод поиска взаимосвязей (ассоциаций) в данных. Поиск подобных взаимосвязей применяется к транзакционным данным в различных отраслях, таких как розничная торговля, банковское дело, страхование. Наиболее распространенный пример – это задача поиска закономерностей в покупаемых вместе товарах. Если вы знаете, какие товары посетители данного магазина покупают вместе, вы можете так расположить продукты в магазине, что продажи вырастут.
Полуконтролируемое обучение
Полуконтролируемое обучение или обучение с частичным участием учителя – это случай, когда обучение происходит на небольшом количестве размеченных и большом количестве неразмеченных данных. Можно сказать, что полуконтролируемое обучение находится между неконтролируемым обучением (без каких-либо размеченных данных) и контролируемым обучением (с полностью размеченными обучающими данными) – см. рис. 1.47.
Рис. 1.47. Полуконтролируемое обучение занимает промежуточное положение между контролируемым и неконтролируемым
Создание размеченных данных для машинного обучения – это длительный процесс, который часто требует квалифицированных специалистов в предметной области и достаточно высоких затрат. Процесс сбора немаркированных данных намного легче и дешевле. Соответственно, затраты на процесс обучения с использованием только размеченных данных могут быть слишком большими, и полуконтролируемое обучение может быть решением проблемы. В последнем случае используются две выборки с данными из одних и тех же классов (размеченная и неразмеченная).
Типичный пример полуконтролируемого обучения – это обучение по фотографиям в социальных сетях, когда есть фото, где пользователь отметил на изображении людей или место съемок, то есть присвоил им теги (разметил данные), а есть фото, где данные не размечены.
Обучение с подкреплением
Машинное обучение с подкреплением напоминает обучение с учителем, однако в данном случае в роли “учителя” выступает окружающая (настоящая или виртуальная) среда, которая показывает, как агенты должны действовать, чтобы получить наибольшее суммарное вознаграждение (рис. 1.48 б ).
Если в случае (рис. 1.48 а ) мы отвечаем на вопрос “К какому классу относится исследуемый объект?”, то в случае (рис. 1.48 б) мы пытаемся ответить на вопрос “Что нужно сделать, чтобы достичь жела-емого результата?”. При этом мы, как правило, не знаем, хороший или плохой выбор мы делаем на каждом шаге, а получаем “вознаграждение” (подкрепление) после завершения эпизода обучения.
Рис. 1.48. Обучение с учителем (а) и обучение с подкреплением (б) имеют сходные схемы.
Еще в 1951 году Марвин Минский, будучи студентом Гарвардского университета, построил машину, использующую простой метод обучения с подкреплением для имитации поведения мышей, которые учатся находить выход из лабиринта.
В качестве примера обучения с подкреплением можно привести компьютерную игровую модель, где агент пытается найти выход из лабиринта и в процессе поиска получает от внешней среды информацию (сигналы подкрепления) о том, где выхода нет, агент анализирует эту информацию и учится находить выход.
Робот (агент) учится выполнять задачу путем повторяющихся проб и ошибок при взаимодействии с незнакомой динамической средой, выполняя определенные действия, получая определенные результаты (и в зависимости от них награды), и при этом его задача – добиваться максимальной награды. Часто, говоря об обучении с подкреплением, в качестве аналогии приводят пример дрессировки домашних животных, которые ориентируются на подкрепление в виде лакомства, которое они получают, выполняя правильные действия.
Аналогично действуют агенты, которые максимизируют метрику вознаграждения за выполнение задачи. При этом следует отметить, что в случае с роботами (агентами) процесс проходит без вмешательства человека и без явного программирования шагов выполнения задачи.
Важным отличием обучения с подкреплением от классического обучения с учителем является то, что подкрепление возникает после нескольких шагов или действий, в то время как в классическом обучении с учителем для каждого обучающего примера известен правильный ответ. Например, при обучении компьютера игре в шахматы методом обучения с подкреплением подкрепление возникает лишь в конце партии – в случае выигрыша или проигрыша.
Мы обещали в начале курса приводить более полные структурные схемы понятия ИИ по мере толкования новых терминов. После того как мы ввели понятия контролируемое обучение, неконтролируемое и обучение с подкреплением, можно несколько усложнить картинку (рис. 1.14), добавив в нее новые элементы (рис. 1.49).
Рис. 1.49. Соотношение базовых направлений в рамках искусственного интеллекта
Соотношение категорий машинного обучения можно также наглядно представить в зависимости от решаемых задач и используемых алгоритмов (рис. 1.50).
Перечень вариантов машинного обучения расширяется. Сравнительно недавно появилась так называемая форма самоконтролируемого обучения (Self-supervised learning SSL).
Самоконтролируемое обучение (предиктивное обучение или самообучение) – это процесс машинного обучения, в котором модель обучается самостоятельно, получая информацию о некоторой части входных данных на основе другой части входных данных (см. рис. 1.51).
Метод самоконтролируемого обучения заключается в определении любой скрытой части входных данных из любой открытой части входных данных. В этом процессе задача из неконтролируемой преобразуется в задачу с контролем путем автоматической генерации меток.
Например, при обработке видео мы можем предсказать прошлые или будущие кадры на основе имеющихся видеоданных.
Рис. 1.51. Предсказание неизвестной части входных данных по другой части ввода.
Продолжая разговор об эволюции систем машинного обучения, следует отметить рост точности и адекватности создаваемых моделей, что, естественно, приводило к повышению доверия к более зрелым моделям со стороны пользователей. Менялись способы создания программного обеспечения, которое обеспечивало решение задач (рис. 1.52).
Рис. 1.52. Эволюция развития ML-проектов как переход от внутренней разработки к внешним сервисам. Источник: адаптировано по материалам SigML Inc
На заре формирования технологии она преимущественно создавалась учеными и исследователями, которые, как правило, совмещали в себе все функции (постановка задачи, разработка алгоритма и непосредственно программирование). Исследования подобного рода велись в рамках научных институтов, университетов, и результаты чаще всего являлись внутренней разработкой, решения не являлись тиражируемым продуктом. На смену периоду разработки систем учеными, которым приходилось в одном лице совмещать все ипостаси, пришли коллективы, с разделением труда.
Разработчики выделились в отдельную категорию, появились специализированные библиотеки, приложения не приходилось писать с нуля, однако дублирование было по-прежнему высоким в силу преобладания внутренних разработок и ограниченного количества общедоступных программных продуктов.
Далее следовал этап продуктивизации. На этом этапе сформировался рынок продуктов как проприетарных, так и с открытым исходным кодом. Выделились профессии, связанные непосредственно с решением отдельных классов задач. На этом этапе все чаще задача исследователей состоит не столько в подборе оптимальной математической модели для описания того или иного набора данных, сколько в выборе доступных продуктов с тем или иным перечнем алгоритмов. Появляются компании, которые все больше услуг выполняют в виде аутсорсинга, крупные корпорации предлагают платформы, которые интегрируют в себе все больше этапов – от сбора данных и их обработки до внедрения моделей для конечных заказчиков. Услуга все чаще предоставляется как экономичный сервис, все большую роль приобретает фактор производительности систем, наличие специализированной инфраструктуры. Кроме того, предоставление модели машинного обучения в качестве сервиса позволяет компаниям монетизировать собранные наборы данных неявным образом, продавая как сервис обученные на этих данных модели.
Например, несмотря на то, что в открытом доступе существуют нейросети для определения эмоций человека по фотографии, предоставляемый облачным провайдером сервис с такой же функциональностью скорее всего позволит добиться большей точности за счет использования проприетарного датасета в процессе обучения.
Более подробно о бизнес-задачах, возникающих в проектах машинного обучения, и типах компаний, вовлеченных в решение данных задач на современном этапе, речь пойдет во второй лекции.
Мы выделили на рис. 1.14 машинное обучение как монолитную область, затем рассмотрели разные научные направления, которые используются для решения задач машинного обучения. Помимо этого, следует упомянуть классификацию машинного обучения по степени контроля за процессом обучения (контролируемое, неконтролируемое, и т. п.), а также по типу целевой переменной и решаемых задач ( рис. 1.42).
Контролируемое обучение (с учителем)
Контролируемое обучение (обучение с учителем) – это подход, при котором алгоритм обучается на входных данных, которые были размечены для решения конкретной задачи. То есть подготовленные для анализа данные изначально содержат ответ, предполагающий правильное действие, которое должна предпринять обучаемая система. Этот процесс мы уже рассмотрели выше, говоря об обучении искусственной нейронной сети.
На рис. 1.42 отмечено два типа задач в категории обучения с учителем – это классификация и регрессия.
Классификация – это одна из наиболее часто встречающихся задач в машинном обучении. Ранее мы рассмотрели использование искусственной нейросети для решения задачи классификации на рис. 1.31. Процесс заключается в том, что на вход сети подаются образцы, вычисляется выходной сигнал, который сравнивается с соответствующим значением целевого вектора (требуемого выхода сети). Векторы обучающего множества последовательно предъявляются обучаемой сети, веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемого уровня. Результатом является обученная модель, способная строить корректные прогнозы в отношении новых неразмеченных данных. Примером может служить распознавание изображений для постановки медицинского диагноза.
При этом нельзя сказать, что успехи нейросетей полностью вытеснили методы классического машинного обучения, включающего в себя целый ряд различных алгоритмов обучения, помимо нейро-сетевого. Нейросети хорошо показывают себя в задачах, где имеются большие объемы данных и признаки трудно извлечь ручным способом. Если же имеются данные небольшого объема с понятными структурированными признаками, то можно применить методы классического машинного обучения, которые мы очень кратко рассмотрим в этом курсе.
В качестве примера алгоритма классического обучения с учителем, используемого для решения задачи классификации, приведем весьма популярный метод опорных векторов (Support Vector Machine, SVM). Впервые этот алгоритм был предложен нашими соотечественниками Владимиром Вапником и Алексеем Червоненкисом в 1963 году.
Идею метода проиллюстрируем на примере задачи определения, к какому из двух изначально известных классов А и Б относится искомый объект.
Рассмотрим простейший наглядный пример (рис. 1.43), где представлены исходные точки (распределенные на плоскости по двум признакам –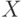
и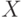 
) и разбитые на два класса “А” и “Б”. Задачей классификации является предсказание принадлежности к тому или иному классу новой (не принадлежащей к известной выборке) точки на плоскости.
Чтобы пример не был абстрактным, скажем, что параметры – это возраст и доход некоторой группы людей, а задача классификации состоит в определении их принадлежности к классу А (потенциальных покупателей определенного товара) и классу Б (тех, кто товар не купит).
На рисунке построена линия, разделяющая эти два класса (разделяющая прямая). Оптимальной с точки зрения точности классификации является прямая, расстояние от которой до каждого класса максимально. Если известно положение данной прямой, то новые точки (не относящиеся к обучающей выборке) будут классифицироваться по положению относительно данной прямой, определяя их принадлежность классу A или Б.
Мы рассмотрели максимально упрощенный пример с двумя признаками. На практике их может быть произвольное число. В общем случае объект представляется вектором в n-мерном пространстве, где координаты вектора описывают его отдельные атрибуты (например, вес, возраст, доход и т. п). В пространствах произвольной размерности вместо прямых рассматривают гиперплоскости – пространства, размерность которых на единицу меньше размерности исходного. Например, в трехмерном пространстве гиперплоскость – это привычно визуализируемая двумерная плоскость.
По обеим сторонам гиперплоскости ( рис. 1.43 б ) строятся параллельные гиперплоскости. Точки данных, лежащие на одной из двух параллельных гиперплоскостей, которые определяют наибольшее расстояние, называются опорными векторами. Отсюда и происходит название метода. Чем больше расстояние между параллельными гиперплоскостями, тем меньше средняя ошибка классификатора.
Представим ситуацию, когда множество точек первого и второго класса пересекаются и разделить их прямой линией невозможно (рис. 1.44). При этом при переходе из двумерного пространства параметров в трехмерное (при добавлении еще одного параметра, являющегося комбинацией имеющихся двух) возникает возможность разнести упомянутые классы и провести искомую плоскость. Таким образом, идея метода SVM состоит в переводе исходных векторов в пространство более высокой размерности и построение гиперплоскости, оптимально разделяющей эти классы.
Для иллюстрации принципа работы алгоритма регрессии, упомянутой на рис. 1.42, рассмотрим линейную регрессию на примере функции одной переменной в задаче прогнозирования стоимости жилья. Предположим, что имеются исходные данные о стоимости жилья определенной площади и нам необходимо спрогнозировать цену квартиры некоторой площади, которую мы планируем приобрести. Графически это можно представить как совокупность точек, которые отражают некоторый тренд. Задача линейной регрессии состоит в том, чтобы провести прямую линию так, чтобы она наиболее точно отражала исследуемый тренд. Зная данный тренд, можно предсказать цену для любой площади.
Прямая описывается уравнением Y = kx+b, и задача определения этой прямой сводится к нахождению параметров (коэффициентов) линейной зависимости (k и b), которые могут быть найдены путем минимизации суммы квадратов отклонений от каждой точки до нашей прямой (метод наименьших квадратов). Определив коэффициенты, мы можем провести прямую, которая обеспечивает минимальные расстояния от этой прямой до исходных точек. Получив уравнение искомой прямой, найдем значение цены квартиры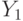
при заданном значении площади 
.
Стоит отметить, что определение коэффициентов может быть сделано как аналитически (метод наименьших квадратов), так и с помощью оптимизационных методов. Для задач большой размерности первый способ оказывается алгоритмически более сложным, поэтому применяются методы градиентной оптимизации, такие как метод градиентного спуска.
Неконтролируемое обучение (без учителя)
К данному типу обучения относятся алгоритмы, которые обучаются на основе набора данных без каких-либо меток. В качестве примера неконтролируемого обучения можно привести кластерный анализ, где стоит задача разделить объекты на классы по неизвестному признаку. В отличие от классификации, в этом случае нет заранее известных классов. Алгоритм сам должен найти похожие объекты и объединить их в кластеры на основе некоторой заданной функции близости. Типичная задача – сегментация покупателей по предпочтениям или лояльности.
Одним из популярных алгоритмов, применяемых для решения задач кластеризации, является метод k-средних – метод, предложенный в 1950-х годах, суть которого состоит в том, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров ( рис. 1.46).
Весьма наглядное толкование метода приводит автор статьи, рассматривая задачу оптимального расположения трех ларьков в поселке. На первом шаге ставим торговые точки случайным образом и смотрим, в какой ларек кому из жителей ближе идти, выделяем три кластера – три группы людей, которым ближе идти до одного из трех ларьков. Перемещаем ларьки в сторону лучшей доступности для посетителей каждой из групп. Повторяем процедуру, то есть опять делим жителей на три кластера и вновь перемещаем ларьки до тех пор, пока не получим решение задачи.
Другой пример, отмеченный на рис. 1.42, – это метод поиска взаимосвязей (ассоциаций) в данных. Поиск подобных взаимосвязей применяется к транзакционным данным в различных отраслях, таких как розничная торговля, банковское дело, страхование. Наиболее распространенный пример – это задача поиска закономерностей в покупаемых вместе товарах. Если вы знаете, какие товары посетители данного магазина покупают вместе, вы можете так расположить продукты в магазине, что продажи вырастут.
Полуконтролируемое обучение
Полуконтролируемое обучение или обучение с частичным участием учителя – это случай, когда обучение происходит на небольшом количестве размеченных и большом количестве неразмеченных данных. Можно сказать, что полуконтролируемое обучение находится между неконтролируемым обучением (без каких-либо размеченных данных) и контролируемым обучением (с полностью размеченными обучающими данными) – см. рис. 1.47.
Создание размеченных данных для машинного обучения – это длительный процесс, который часто требует квалифицированных специалистов в предметной области и достаточно высоких затрат. Процесс сбора немаркированных данных намного легче и дешевле. Соответственно, затраты на процесс обучения с использованием только размеченных данных могут быть слишком большими, и полуконтролируемое обучение может быть решением проблемы. В последнем случае используются две выборки с данными из одних и тех же классов (размеченная и неразмеченная).
Типичный пример полуконтролируемого обучения – это обучение по фотографиям в социальных сетях, когда есть фото, где пользователь отметил на изображении людей или место съемок, то есть присвоил им теги (разметил данные), а есть фото, где данные не размечены.
Обучение с подкреплением
Машинное обучение с подкреплением напоминает обучение с учителем, однако в данном случае в роли “учителя” выступает окружающая (настоящая или виртуальная) среда, которая показывает, как агенты должны действовать, чтобы получить наибольшее суммарное вознаграждение (рис. 1.48 б ).
Если в случае (рис. 1.48 а ) мы отвечаем на вопрос “К какому классу относится исследуемый объект?”, то в случае (рис. 1.48 б) мы пытаемся ответить на вопрос “Что нужно сделать, чтобы достичь жела-емого результата?”. При этом мы, как правило, не знаем, хороший или плохой выбор мы делаем на каждом шаге, а получаем “вознаграждение” (подкрепление) после завершения эпизода обучения.
Еще в 1951 году Марвин Минский, будучи студентом Гарвардского университета, построил машину, использующую простой метод обучения с подкреплением для имитации поведения мышей, которые учатся находить выход из лабиринта.
В качестве примера обучения с подкреплением можно привести компьютерную игровую модель, где агент пытается найти выход из лабиринта и в процессе поиска получает от внешней среды информацию (сигналы подкрепления) о том, где выхода нет, агент анализирует эту информацию и учится находить выход.
Робот (агент) учится выполнять задачу путем повторяющихся проб и ошибок при взаимодействии с незнакомой динамической средой, выполняя определенные действия, получая определенные результаты (и в зависимости от них награды), и при этом его задача – добиваться максимальной награды. Часто, говоря об обучении с подкреплением, в качестве аналогии приводят пример дрессировки домашних животных, которые ориентируются на подкрепление в виде лакомства, которое они получают, выполняя правильные действия.
Аналогично действуют агенты, которые максимизируют метрику вознаграждения за выполнение задачи. При этом следует отметить, что в случае с роботами (агентами) процесс проходит без вмешательства человека и без явного программирования шагов выполнения задачи.
Важным отличием обучения с подкреплением от классического обучения с учителем является то, что подкрепление возникает после нескольких шагов или действий, в то время как в классическом обучении с учителем для каждого обучающего примера известен правильный ответ. Например, при обучении компьютера игре в шахматы методом обучения с подкреплением подкрепление возникает лишь в конце партии – в случае выигрыша или проигрыша.
Мы обещали в начале курса приводить более полные структурные схемы понятия ИИ по мере толкования новых терминов. После того как мы ввели понятия контролируемое обучение, неконтролируемое и обучение с подкреплением, можно несколько усложнить картинку (рис. 1.14), добавив в нее новые элементы (рис. 1.49).
Соотношение категорий машинного обучения можно также наглядно представить в зависимости от решаемых задач и используемых алгоритмов (рис. 1.50).
Перечень вариантов машинного обучения расширяется. Сравнительно недавно появилась так называемая форма самоконтролируемого обучения (Self-supervised learning SSL).
Самоконтролируемое обучение (предиктивное обучение или самообучение) – это процесс машинного обучения, в котором модель обучается самостоятельно, получая информацию о некоторой части входных данных на основе другой части входных данных (см. рис. 1.51).
Метод самоконтролируемого обучения заключается в определении любой скрытой части входных данных из любой открытой части входных данных. В этом процессе задача из неконтролируемой преобразуется в задачу с контролем путем автоматической генерации меток.
Например, при обработке видео мы можем предсказать прошлые или будущие кадры на основе имеющихся видеоданных.
Продолжая разговор об эволюции систем машинного обучения, следует отметить рост точности и адекватности создаваемых моделей, что, естественно, приводило к повышению доверия к более зрелым моделям со стороны пользователей. Менялись способы создания программного обеспечения, которое обеспечивало решение задач (рис. 1.52).
На заре формирования технологии она преимущественно создавалась учеными и исследователями, которые, как правило, совмещали в себе все функции (постановка задачи, разработка алгоритма и непосредственно программирование). Исследования подобного рода велись в рамках научных институтов, университетов, и результаты чаще всего являлись внутренней разработкой, решения не являлись тиражируемым продуктом. На смену периоду разработки систем учеными, которым приходилось в одном лице совмещать все ипостаси, пришли коллективы, с разделением труда.
Разработчики выделились в отдельную категорию, появились специализированные библиотеки, приложения не приходилось писать с нуля, однако дублирование было по-прежнему высоким в силу преобладания внутренних разработок и ограниченного количества общедоступных программных продуктов.
Далее следовал этап продуктивизации. На этом этапе сформировался рынок продуктов как проприетарных, так и с открытым исходным кодом. Выделились профессии, связанные непосредственно с решением отдельных классов задач. На этом этапе все чаще задача исследователей состоит не столько в подборе оптимальной математической модели для описания того или иного набора данных, сколько в выборе доступных продуктов с тем или иным перечнем алгоритмов. Появляются компании, которые все больше услуг выполняют в виде аутсорсинга, крупные корпорации предлагают платформы, которые интегрируют в себе все больше этапов – от сбора данных и их обработки до внедрения моделей для конечных заказчиков. Услуга все чаще предоставляется как экономичный сервис, все большую роль приобретает фактор производительности систем, наличие специализированной инфраструктуры. Кроме того, предоставление модели машинного обучения в качестве сервиса позволяет компаниям монетизировать собранные наборы данных неявным образом, продавая как сервис обученные на этих данных модели.
Например, несмотря на то, что в открытом доступе существуют нейросети для определения эмоций человека по фотографии, предоставляемый облачным провайдером сервис с такой же функциональностью скорее всего позволит добиться большей точности за счет использования проприетарного датасета в процессе обучения.
Более подробно о бизнес-задачах, возникающих в проектах машинного обучения, и типах компаний, вовлеченных в решение данных задач на современном этапе, речь пойдет во второй лекции.
-
Add a note